Game Theory: What’s PaaS Got To Do With It?

Let’s say you own this bike:

Your friend Gemma wants to buy it from you. She’s willing to pay up to £50 for it. You don’t want to tell Gemma this but you know the bike is on its last legs. You’ll happily accept £5 for it, though no less than that. Since Gemma places a higher value on the bike there is a surplus to be gained if the transaction were to take place. The maximum surplus available is £45. How much should Gemma offer to pay for this bike?

I’m sure you’re wondering what is the deal with this story about a bike?

I’ve been working on the Cloud Foundry team at Pivotal for just over 6 months now. It’s been a tough domain to sink my teeth into but I’ve been enjoying the challenge. I’ve been using some of my spare time to read into some of the concepts at a deeper level. When you don’t understand something, one thing to try and do is frame the concepts in terms you are familiar with. For me, I can appeal to Game Theory.

I studied Economics at university and Game Theory, the study of strategic interactions between rational agents, was my favourite paper. I loved how examples of it extended beyond economics to politics, biology, and other day-to-day interactions.

The story about the bike above can be modelled as a game. There are two players: yourself and Gemma. You both have your strategy sets. For Gemma, this is a list of prices that she could offer you for your bike. For you, it’s a list of prices that you will accept for your bike. Gemma’s payoff will be derived from how much she ends up paying for the bike relative to her £50 valuation — we can assume that her utility is increased the less she has to pay. Your payoff will be derived from how much you receive for your bike relative to it’s value to you — the more you’re paid for it, the happier you are.

Bargaining Theory is a branch of Game Theory that attempts to give a specific answer to the following question: at which price will this transaction take place?

John Nash came up with one way to answer this question. He modelled bargaining as a cooperative game, meaning that players can coordinate their actions before the game begins. He also had further assumptions about how utility functions behaved, including that if the utility functions for players are identical each should receive the same outcome.

In relation to the bike example, the Nash Bargaining Solution (NBS) may say something like: given yours and Gemma’s utility functions, the transaction will take place at a price of £20, giving you £15 worth of surplus and Gemma £30 worth of surplus.

But what has Platform-as-a-Service got to do with all of this?

Moving away from monetary terms and framing the issues in terms of surplus we can more easily model complex interactions between more than two agents and look at the distribution of surplus between them.

Let’s  model a simple resource allocation problem — we can look at this as a cooperative game. The computers in the system have different capabilities and so need to work together to most efficiently handle an incoming stream of jobs. Computers with heavier loads are worse off:

• The players are the computers

• Each computer has a different processing rate, x (jobs/sec)

• The actions of each computer are represented by how many incoming jobs they accept, y (jobs/sec)

• The payoff to each computer is a function of their load

Let’s take a large distributed system of 2 computers, where:

 

T represents the rate of incoming jobs to the system.

Here is a diagram to show what’s going on here:

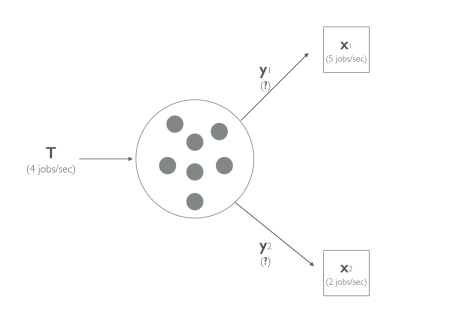We want to find the values of y that optimally minimises the time taken for the computers to execute the jobs. Optimal here means that we cannot improve the performance of one computer without reducing the performance of another once we’ve arrived at a final distribution.

 

We need a queuing system to help us find a way to model the utilities of the computers. We then need to aggregate the utility functions and find the values of y that maximises the utility for each machine. Based on the utility function shown in the image above, we get a solution that looks something like this:

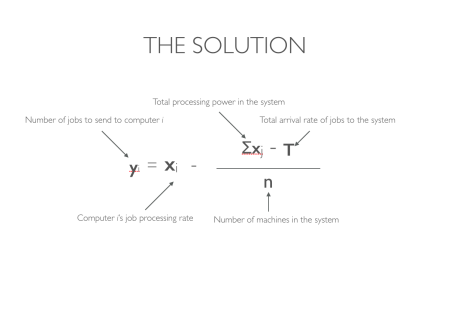One way of phrasing the solution is like so: the number of jobs to send to any given computer is equal to its processing rate minus the average excess processing capacity.

Back to our large distributed system. Substituting in the processing rates gives us the following results:

Every second, we should send 3.5 jobs to the computer that can handle a maximum of 5 and 0.5 jobs to the computer that can handle a maximum of 2.

Approaching the problem like this leads us to a NBS.  Earlier I  mentioned how the NBS can help us find the unique point when two agents are negotiating. We can extrapolate that with n players as shown in a paper by Daniel Grosu on this topic.

Say we had ten computers in the system and one returned a negative value for the number of jobs it would accept. One way of looking at the negative value is to say that the computer in question performs too slowly and should be removed from the system before we then redo the calculations. We continually repeat the calculation until all remaining computers in the system have a positive y. The final outcome will represent the unique bargaining point as dictated by the NBS. We can use results like this to develop algorithms that dynamically distribute loads amongst computers in a system.

What assumptions are implicit in this example? Among many:

• We’ve assumed that all jobs are identical entities — what about deadlines or priorities?
• The queuing theory used is very unrealistic for real computer systems — it implies that time taken to service jobs increases exponentially

Keeping the assumptions in mind, we can tweak the inputs and see how that affects our output. By continually playing around with these calculations we can learn more about how different characteristics of the elements of a system will interact.

You don’t need maths to use Game Theory as a tool to understand complex issues. As a starting point, just think about how you would model parts of your system as a game and what form of competition or cooperation needs to happen between the components.

For the mathematical out there, exploring Game Theory opens up a world of interesting algorithms to help us produce better performing systems.

If you want to delve deeper into the maths that I hinted at in this post then have a look at ‘Load Balancing in Distributed Systems: A Game Theoretic Approach‘ by Daniel Grosu. For a brilliant read introducing you to how Game Theory reveals itself in our day-to-day life then I wholeheartedly recommend ‘Thinking Strategically‘ by Avinash Dixit and Barry Nalebuff.

This blog post was adapted from a lightning talk given at the London PaaS User Group. You can find the slides on SlideShare.